Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;May 26, · First, remember that graphs of functions of two variables, z = f (x,y) z = f ( x, y) are surfaces in three dimensional space For example, here is the graph of z =2x2 2y2 −4 z = 2 x 2 2 y 2 − 4 This is an elliptic paraboloid and is an example of a quadric surface We saw several of these in the previous sectionFeb 05, 13 · Find the maximum rate of change of f(x,y)= ln (x^2 y^2) at the point (1, 4) and the direction in which it occurs 1) Maximum rate of change = 2)

Find The Local Linear Approximation L To The Function F X Y Ln Xy At The Point P 1 2 Compare The Brainly In
F(x y)=ln(x^2+y^2)
F(x y)=ln(x^2+y^2)-Jul 05, 09 · For this one we need the log rule, chain rule and the power rule y = ln (x^2 y^2) dy/dx = 1/ (x^2 y^2) * (2x 2y (dy/dx)) dy/dx = (2x 2y dy/dx) / (x^2 y^2) We need to split the fraction so that all the dy/dx terms can be on the leftThe first derivative of mathz/math with respect to mathx/math is math\frac {\partial z}{\partial x}=\frac {2x}{x^2y^2}/math The second derivative is



Complex Analysis Gamelin Ii 5 Problems And Solutions Derivative Trigonometric Functions
(b) f(x,y) = 2x2 xy2 −2, D= {(x,y) ∈ R2;x2 y2 64} Solution (a) Calculating the partial derivatives gives f x = y 2 √ x − 1, f y = √ x−2y 6 Finding critical points f x = 0, f y = 0 =⇒ (x,y) = (4,4) Note that (4,4) ∈ Dand that f(4,4) = 12 The boundary of Dconsists of four line segments1) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withMar 11, 07 · Show in 2 ways that the function ln(x^2y^2) is harmonic in every domain that does not contain the origin My problem with this quesiton is firstly, I don't know two ways, because normally I would do CauchyRiemann equations but there is no real/imaginary numbers so I don't know what is u(x,y) and what is v(x,y) As a function I know that if I differentiate in terms of x I get
Free multi variable limit calculator solve multivariable limits stepbystepGet an answer for 'Show that z=ln((x^2) (y^2)) is a solution of Laplace's equation δ^2z/δx^2 δ^2/δy^2 = 0' and find homework help for other Math questions at eNotesIf we have f (x, y) = \ln (x^2 y^2) Note that the y term is missing here, and using the chain rule with \ln, we get d/dx ~ (\ln (x^2 y^2)) = \dfrac {1} {x^2 y^2}~d/dx~ (x^2 y^2) = \dfrac {1} {x^2 y^2} (2x0) =\dfrac {2x} {x^2 y^2}
E y = x Then base e logarithm of x is ln(x) = log e (x) = y The e constant or Euler's number is e ≈ Ln as inverse function of exponential function The natural logarithm function ln(x) is the inverse function of the exponential function e x For x>0, f (f 1 (x)) = e ln(x) = x Or f 1 (f (x)) = ln(e x) = x NaturalApr , 21 · Find local max point of f (x,y) = ln (x^2 y^2 1) Use gradient descent method$f(x,y)$ is the composition of two functions If $g(x,y) = x^2 y^2$ and $h(s) = \ln(s)$ then $f(x,y) = h(g(x,y))$ $g(x,y)$ is continuous for all $x$ and $y$ What is the range of $g(x,y)?$ For what values of $s$ in the range of $g(x,y)$ is $h(s)$ not continuous?



Solved Evaluate Partial Differential U Partial Differenti Chegg Com



Find The Local Linear Approximation L To The Function F X Y Ln Xy At The Point P 1 2 Compare The Brainly In
F(x, y, z) = z tan −1 (y 2)i z 3 ln(x 2 4)j zk Find the flux of F across S, the part of the paraboloid x 2 y 2 z = 30 that lies above the plane z = 5 and is oriented upward S F · dS = Expert Answer Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorFind dy/dx y = natural log of x^2y^2 y = ln (x2 y2) y = ln ( x 2 y 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2 y2)) d d x ( y) = d d x ( ln ( x 2 y 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsAnswer to Let f(x, y) = ln (x^2 y^2) Which one of the following curves is a simple closed path in the domain of the function f ?



F X Ln X 4 Domain Range Graph And Its Inverse Youtube



Complex Analysis Gamelin Ii 5 Problems And Solutions Derivative Trigonometric Functions
Oct 13, 16 · Homework Statement for the domain of ln (x^2 y^2 ) , it it given in my notes that the ans is x ≠ 0 and y ≠ 0 IMO , it's wrong to give x ≠ 0 and y ≠ 0 , because the meaning of x ≠ 0 and y ≠ 0 is that x and y cant be 0 all the times so just leave the ans (x^2 y^2 ) > 0 , will do(a) f(x;y) = p x2 y2 1 ln(4 x2 y2) The function is de ned for x 2 y 1 0 and 4 x2 y2 0 The domain is D = f(x;y) 2R2j1 x2 y2 < 4g This is an annular region in the xyplane (b) f(x;y) = p x p y p x2 y2 16 The function is de ned for x 0, y 0, and x2 y2 16 0 The domain is D = f(x;y) 2R2jx 0;yF(x, y) = xyln(x2 y2) = rcosθrsinθln(r2) = r2lnrsin(2θ) = g(r, θ) The partial derivatives of g are given by ∂g ∂r = r(2lnr 1)sin(2θ), ∂g ∂θ = 2r2lnrcos(2θ) Since r > 0 and sin2θ > 0 in our range, the equation ∂g ∂r = 0 implies that 2lnr 1 = 0 or r = e − 1 2
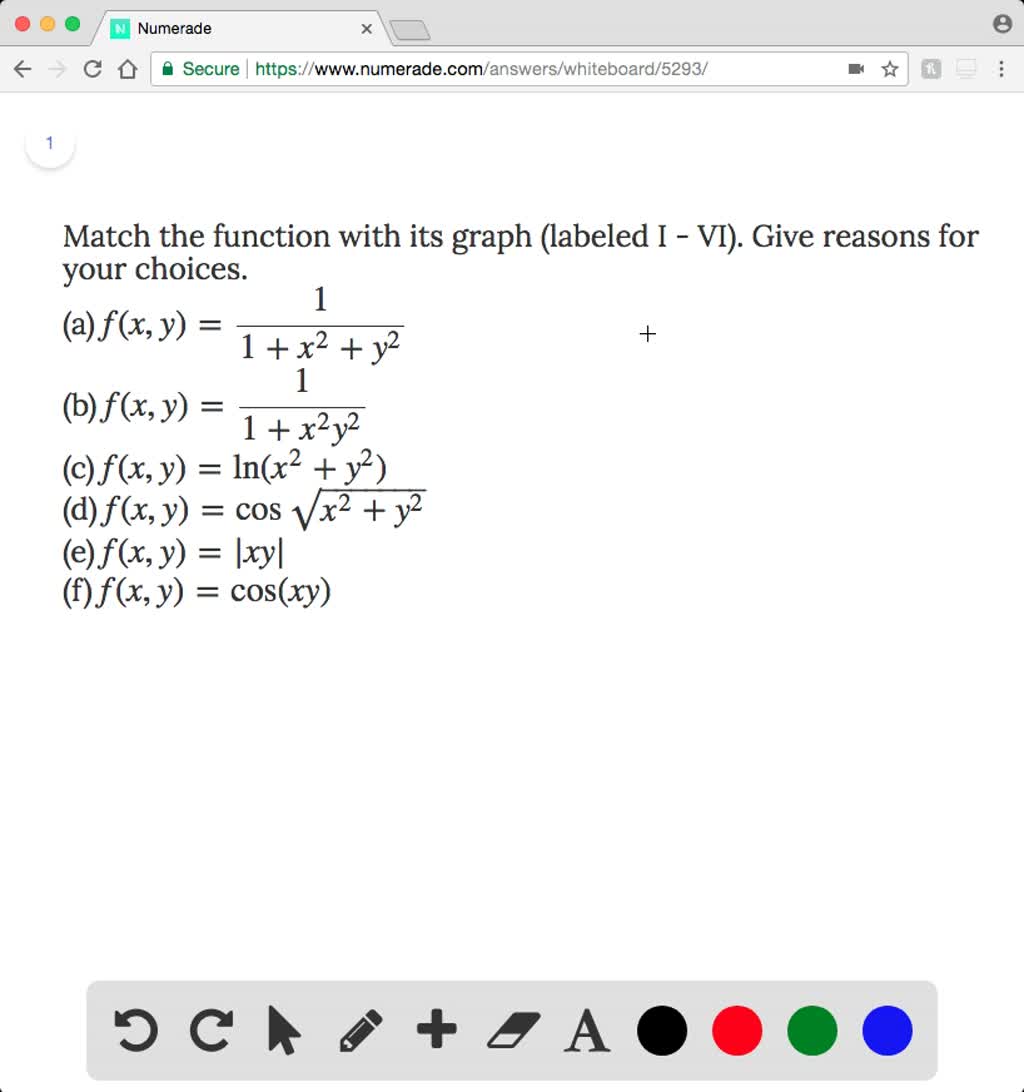


Solved Match The Function With Its Graph Labeled



Math 6c Chapter 12 Quiz
Solution Simplify rst ln p x2 y2 = (1=2)ln(x2 y2) Then f x = (1=2)(1=(x2 y2))(2x) = x=(x2 y2) By symmetry, f y = y=(x2 y2) Di erentiating again (using the quptient rule), one determines that f xx = (x2 y2) 2x2 (x2 y2)2 = y2 x2 (x2 y2)2 By symmetry, f yy = (x2 y2)=(x2 y2)2 And so, f xx f yy = 0First of all, let us check the domain of mathy = \ln (3x^2 4x5)/math For this purpose, suppose mathf(x) = 3x^2 4x5/math Here coefficient of mathx^2=3A The given function is f(x,y)=ey in the interval x belongs to 0,8 and y belongs to 0,ln2 question_answer Q The region is formed by the graphs of y 4x and y 12x



How Do You Implicitly Differentiate Xy 2 Xcos Xy Ln X Y Ytan Xy Homeworklib
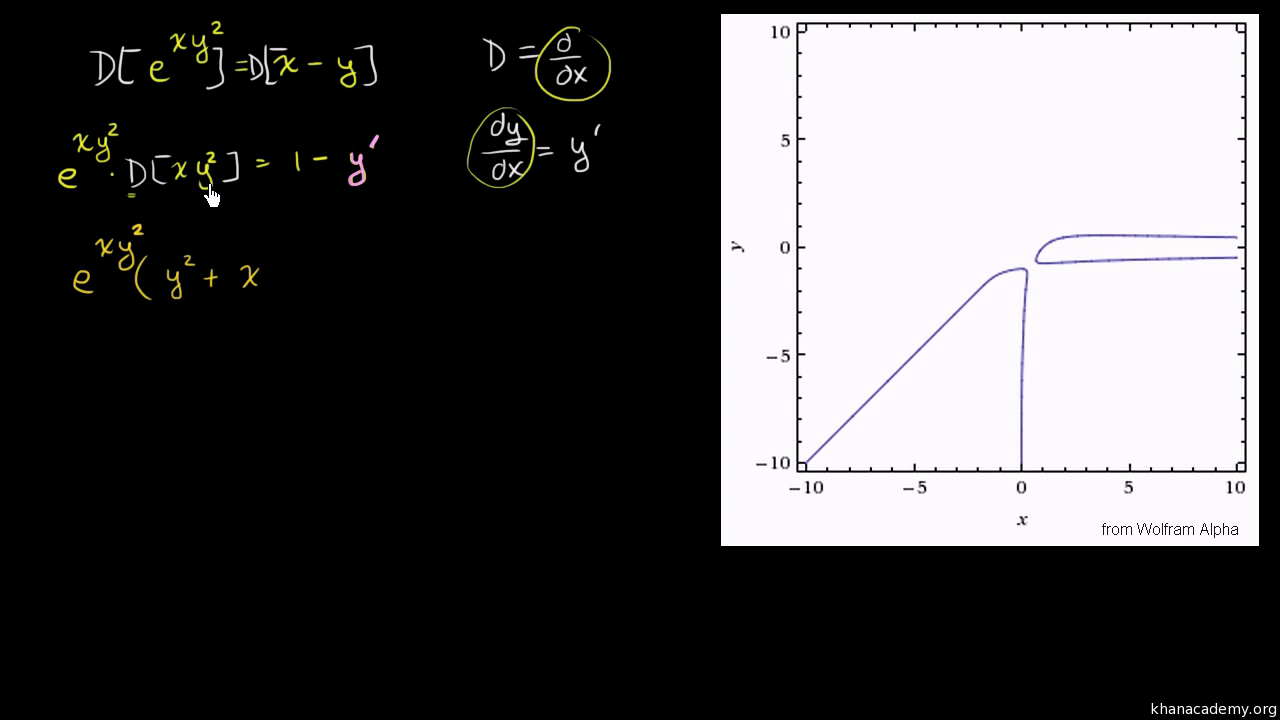


Implicit Differentiation Advanced Example Video Khan Academy
```(dz)/(dx) = 1/sqrt(x^2 y^2) (d/(dx) sqrt(x^2 y^2))` since `d/(dx) ln(f(x)) = (f'(x))/f(x)` `d/(dx) sqrt(x^2 y^2) = (1/2)(x^2y^2)^(1/2)(2x) = x/sqrt(x^2y^2)`121/x (1) ln 121/x dy dx =y − 1 x 21/xln2 121/x ln 121/x dy dx = 12 1/x x 1SeanA(x 1,y 1),B(x 2,y 2),M(3,−1)y−→v =F x y z ln x 2 y 2 z en p 111 f x y z ln x 2 y 2 z en p 111 fx zy e xy f y zx e from CALCULO II at National Open and Distance University



Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange
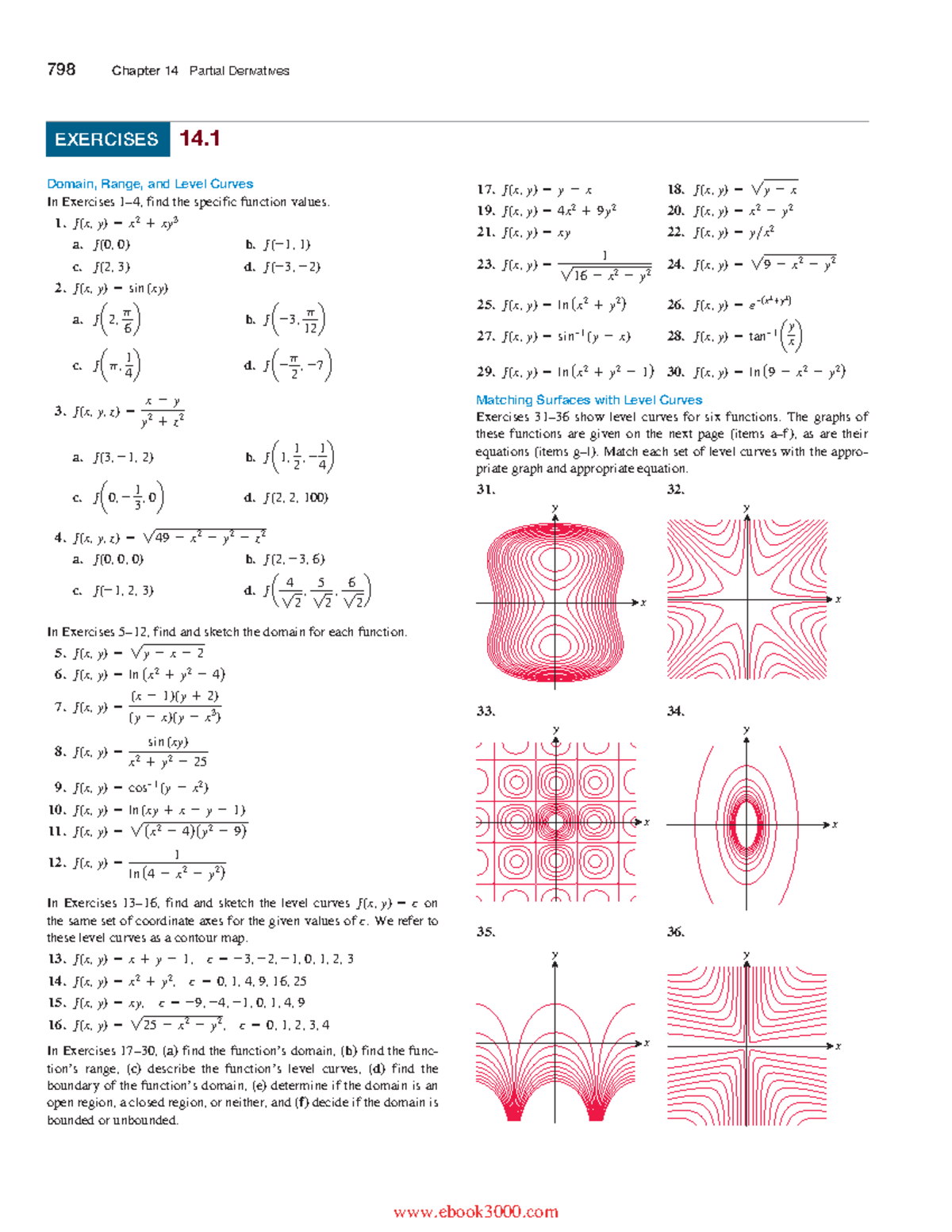


Ejercicios 4 Cvv Holi Matg1002 Studocu
Solution for Suppose f(x, y) = ln(x^2 y^2 ) A Compute each of the following partial derivatives (iv) ∂^2f ∂y^2 (x, y) = B Verify that ∂^2f/∂x^2 (x, y)Aug 01, 01 · The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2718 281 8 459The natural logarithm of x is generally written as ln x, log e x, or sometimes, if the base e is implicit, simply log x Parentheses are sometimes added for clarity, giving ln(x), log e (x), or log(x)View full document (a) f ( x, y ) = ln ( x 2 y 2 9 ) (b) f ( x, y ) = ( x 1) ( y 2) ( y x ) ( y x 2 ) 4 Consider the function f ( x, y ) = p x 2 3 x y (a) Determine the domain of f ( x, y ) (b) Sketch the domain of f , and the level curve that passes through P = ( 2 , 6) (c) Find the value c such that f



Solved If F X Y Ln Y Then Nabla F X Y 1 Y Let F Chegg Com


1 Determine The Domain For The Following Function And Draw The Graph In Xy Plane F X Y Ln X Y 2 8 Marks 2 For Z F X Y E4x2 9y14m Course Hero
Instead, we first simplify with properties of the natural logarithm We have ln (1 x) (1 x 2) 2 (1 x 3) 3 = ln (1 x) ln (1 x 2) 2 ln (1 x 3) 3 Now the derivative is not so daunting We have use the chain rule to get We define logarithms with other bases by the change of base formulaCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history函数f (x)=ln (x1)/根号下1x的定义域为 1年前 1个回答 求下列函数的微分求下列函数的微分:1.y=xarctan2x2y=ln (1x^2)/ (1x^2)3y= (根号下 ( 1年前 2个回答 y=ln根号下 (1x)^e^x/arccosx求导 1年前 1个回答 高数 已知参数方程 {x=ln根号下1t的平方,y=arctant},求二阶导



Functions Inverses Ppt Download



Solved 2 Find The First Partial Derivatives For The Fun Chegg Com
(f) f(x;y)=x3 arcsiny2 Solution The arcsin requires the input y 2 between − 1 and 1, which is equivalent to − 1 y 1 So the range is the in nite horizontal strip between the lines y = − 1Integrate F(x,y) = Ln(x^2y^2)/sqrt{x^2y^2} Over The Region 1 Leq X^2y^2 Leq E^{10} Question Integrate F(x,y) = Ln(x^2y^2)/sqrt{x^2y^2} Over The Region 1 Leq X^2y^2 Leq E^{10} This problem has been solved!Any real function u(x, y) with continuous second partial derivatives which satisfies Laplace's equation, ∇2u(x, y) = 0 is called a harmonic function z(x, y) = ln(x2 y2) ∇2z(x, y) = ∂2z ∂x2 ∂2z ∂y2 you can solve the above expression and it must equal to 0 to be satisfied for the harmonic function Share answered Mar 28 '16 at 642



Derivada Logaritmo Ln X Sqrt 1 X 2 Youtube



Implicit And Logarithmic Differentiation
Answer and Explanation Given that f(x, y) = ln(1 x2y2) f ( x, y) = ln ( 1 x 2 y 2) Partially differentiating with respect to x we obtain fx = ∂ ∂x(ln(1 x2y2)) ⇒ fx = 1 (1 x2y23 For each solution ( x,y,z,,µ), find f(x,y,z) and compare the values you get The largest value corresponds to maximums, the smallest value corresponds to minimums 5 Examples Example 51 Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints xy z =0and x2 2z2 =1 f(x,y,zOn f(x 2 y 2) = f(x) 2 f(y) 2 Consider an integervalued function f(k) such that f(1) is positive and We can show that the only such function is the identity function f(k) = k To prove this, first note that setting m = 1 and n = 0 in equation (1) and rearranging terms gives the condition
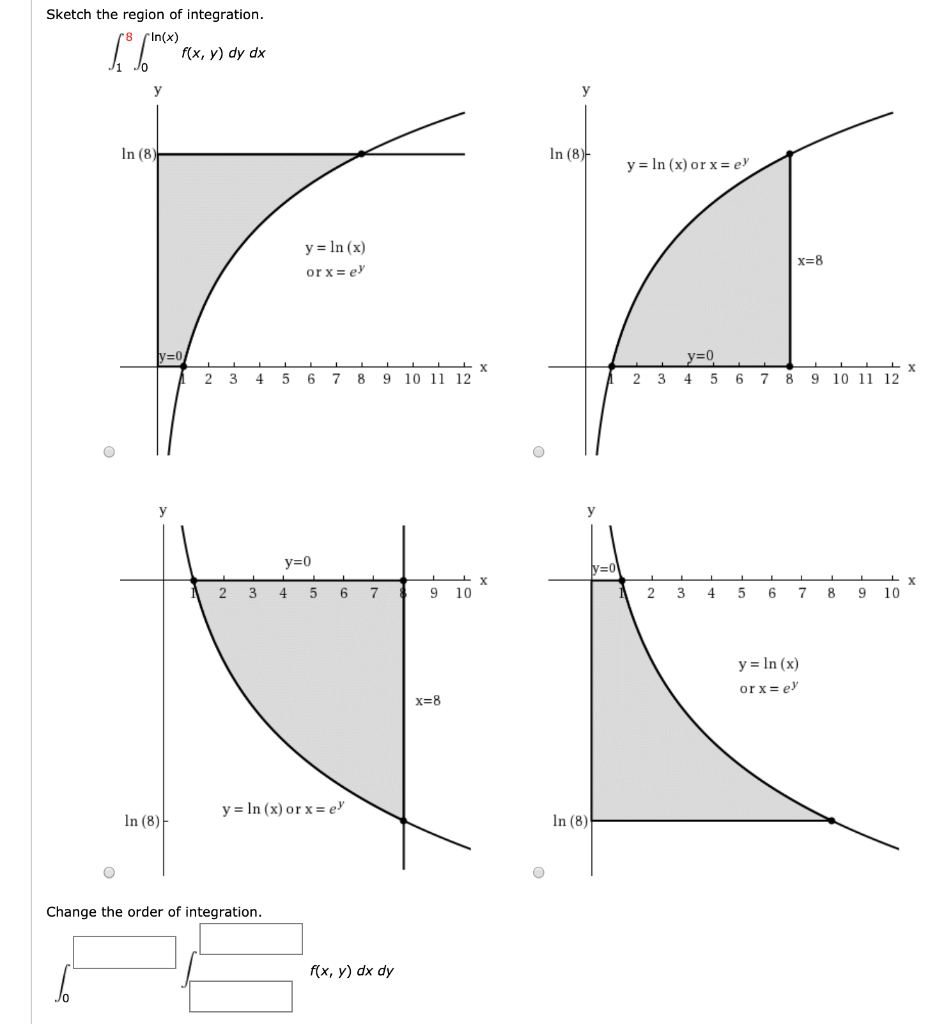


Solved Sketch The Region Of Integration 8 Pin X F X Y Chegg Com


Solved Ln Xy Y 2 And To The Variables X Y Defined By X E 2t Y E 2t A Make A Variable Diagram B Finally On How Many Variables Does The Variable Course Hero
Consider f(x, y)=\ln \left(x^{2}y^{2}\right) Show that f is a solution of the partial differential equation \frac{\partial^{2} f}{\partial x^{2}}\frac{\par Ask your homework questions to teachers and professors, meet other students, and be entered to win $600 or an Xbox Series X 🎉Oct 09, 15 · It depends on whether we need d/dx or d/dt For d/dt d/dt(ln(x^2y^2)) = 1/(x^2y^2) d/dt(x^2y^2) = 1/(x^2y^2) * (2xdx/dt 2y dy/dt) For d/dx d/dx(ln(x^2y^2)) = 1/(x^2y^2) d/dx(x^2y^2) = 1/(x^2y^2) * (2x 2y dy/dx) Calculus Science Anatomy & Physiology AstronomyGraph y = natural log of 9x^2 y = ln (9 − x2) y = ln ( 9 x 2) Find the asymptotes Tap for more steps Set the argument of the logarithm equal to zero 9 − x 2 = 0 9 x 2 = 0 Solve for x x Tap for more steps Subtract 9 9 from both sides of the equation
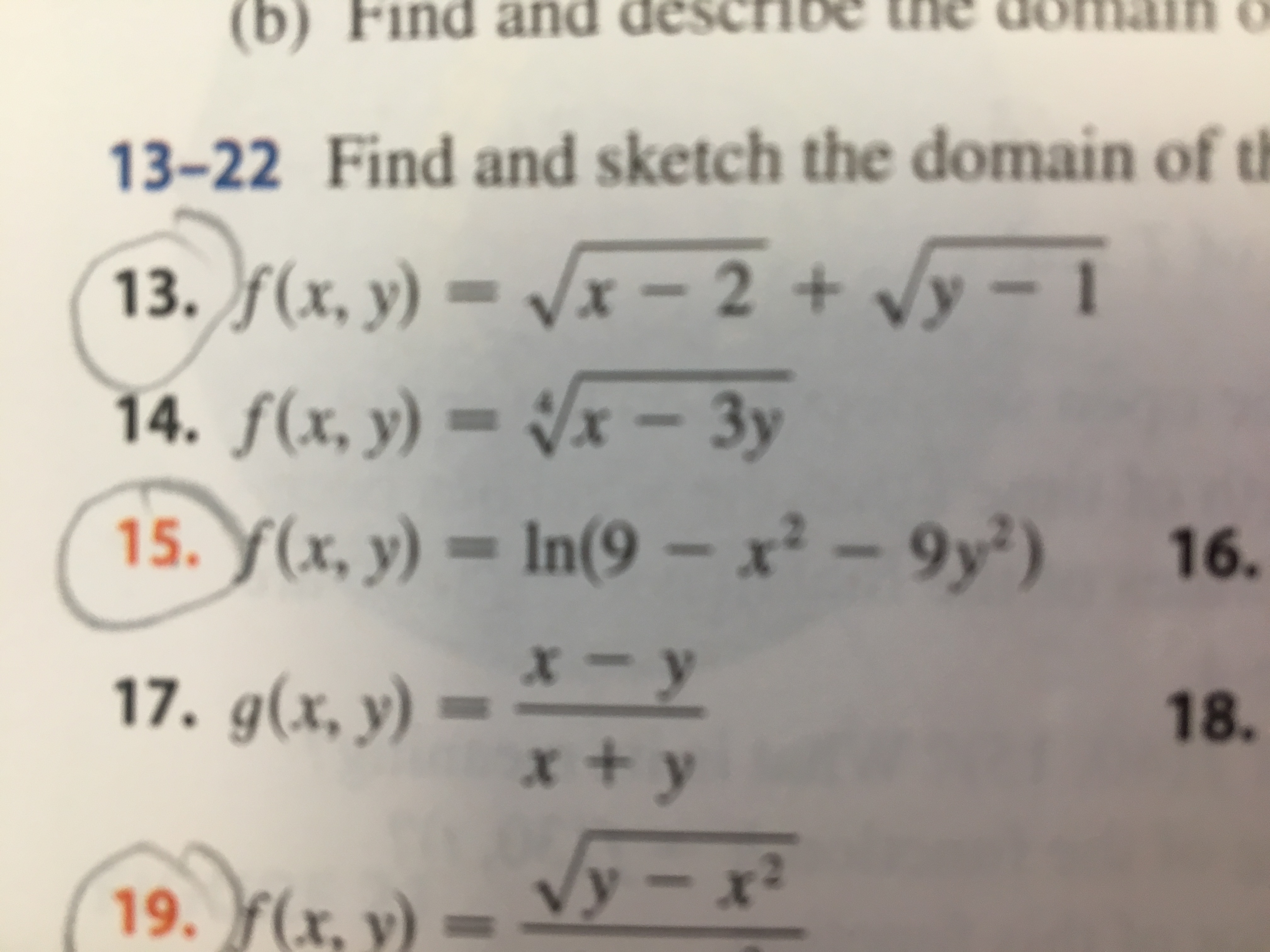


Answered B Find And Describe The Do 13 22 Find Bartleby



First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Youtube
Homework 5 Solutions 3132 f(x;y)=œ xy(x2−y2) x2y2 (x;y)≠(0;0) 0 (x;y)=(0;0) Note fis continuous, (by computing lim(x;y)→(0;0) of the formula above, eg using polar coorinates) (a) Find f x and f y when (x;y)≠(0;0) Away from (0;0);fcan be di erentiated using the formula de ning it,Determine the region of the x yplane x yplane in which f (x, y) = ln (x 2 y 2 − 1) f (x, y) = ln (x 2 y 2 − 1) is continuous Use technology to support your conclusion (Hint Choose the range of values for x and y x and y carefully!)Cancel out x in both numerator and denominator \frac {2\left (x^ {2}2xyy^ {2}\right)} {x\left (yx\right)y^ {2}} x ( y − x) y 2 − 2 ( x 2 − 2 x y y 2) Factor the expressions that are not already factored Factor the expressions that are not already factored



Solved Given The Equation Y Ln X 2 Y 4 5 8 Evalua Chegg Com



Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube
Multivariable Calculus Find the linear approximation to the function f(x, y) = x^2 y^2 x at the point (2, 3) Then approximate (21)^2 (29)^2 21ForSep 14, 17 · # F(x,y) = ln(x^2y^2) y # We have # (partial F)/(partial x) = (2x)/(x^2y^2) # # (partial F)/(partial y) = (2y)/(x^2y^2) 1 = (x^2y^22y)/(x^2y^2)# Then # dy/dx = ((partial F)/(partial x)) / ((partial F)/(partial y)) # # \ \ \ \ \ \ = ((2x)/(x^2y^2)) / ((x^2y^22y)/(x^2y^2)) # # \ \ \ \ \ \ = (2x) / (x^2y^22y) #Ex 1456 Suppose the electric potential at $(x,y)$ is $\ds\ln\sqrt{x^2y^2}$ Find the rate of change of the potential at $(3,4)$ toward the origin and also in a direction at a right angle to the direction toward the origin



Solved Find The Critical Point Of The Function F X Y Chegg Com



Differential Equations Separation Of Variables Ppt Download
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Ejercicios De Calculo Vectorial Pagina 2 Monografias Com



Find Y X If It Satisfies The Following Differential Equation



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby



Let F X Ln 1 X 1 X Find X Y For Which F X F Y F X Y



Contour Map Of F X Y 1 X 2 Y 2 Youtube



Solved Question 22 Find And Sketch The Domain Of The Func Chegg Com



14 2 Limits And Continuity



Lagrange Multipliers Minimize F X Y X 2 Y 2 Subject To X 2y 5 0 Youtube
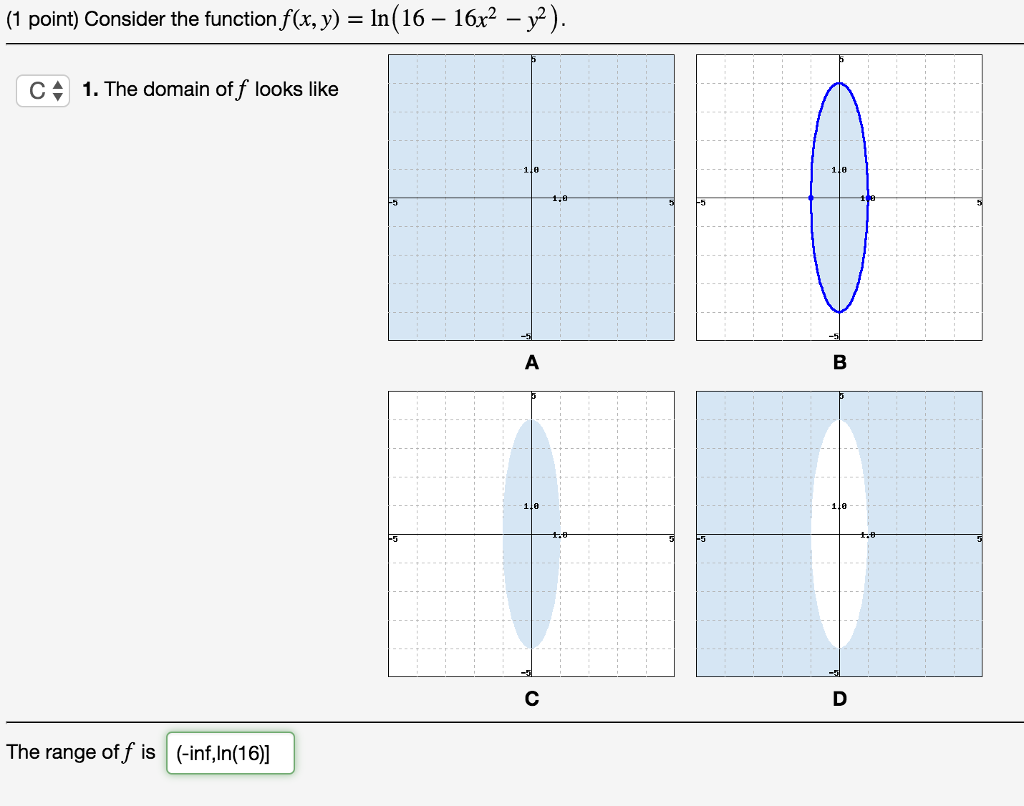


Solved Consider The Function F X Y Ln 16 16x 2 Y Chegg Com



2 Partial Differentiation



Solutions F X 6x 2 6xy 24x F Y 3x 2 6y To Find The Critical Points We Solve Pdf Free Download



Partial Differentiation And Multiple Integrals Pdf Free Download



Multivariable Calculus Finding And Sketching The Domain Youtube



Max And Min X Y Ln X 2 Y 2 Mathematics Stack Exchange



Find The Average Value Of F X Y 1 Xy Over The Square Ln 2 Leq X Leq 2 Ln 2 Ln 2 Leq Y Leq 2 Ln 2 Homework Help And Answers Slader



Calc 501 1000 By James Bardo Issuu



Implicit Differentiation Advanced Example Video Khan Academy



Ln Xy Ln X Ln Y



Solutions Problem 1 Find The Critical Points Of The Function F X Y



Economics 121b Intermediate Microeconomics Problem Set 2 1 10 Pdf Free Download



What Is The Equation Of The Tangent Line Of F X Ln X 3 X 7x At X 3 Socratic



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com



Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange



Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange



Solved 1 A Let Z Ln X 2xy Where X 25 St And Chegg Com


Larson Calculus 13 3 28 First Partial Derivatives Of G X Y Ln Sqrt X 2 Y 2 Youtube



Practice Problems 10 And 11



Derivative Of F X Sqrt Ln X Math Videos Calculus Chain Rule


Implicit And Logarithmic Differentiation



Answered 53 58 Find All The Second Partial Bartleby
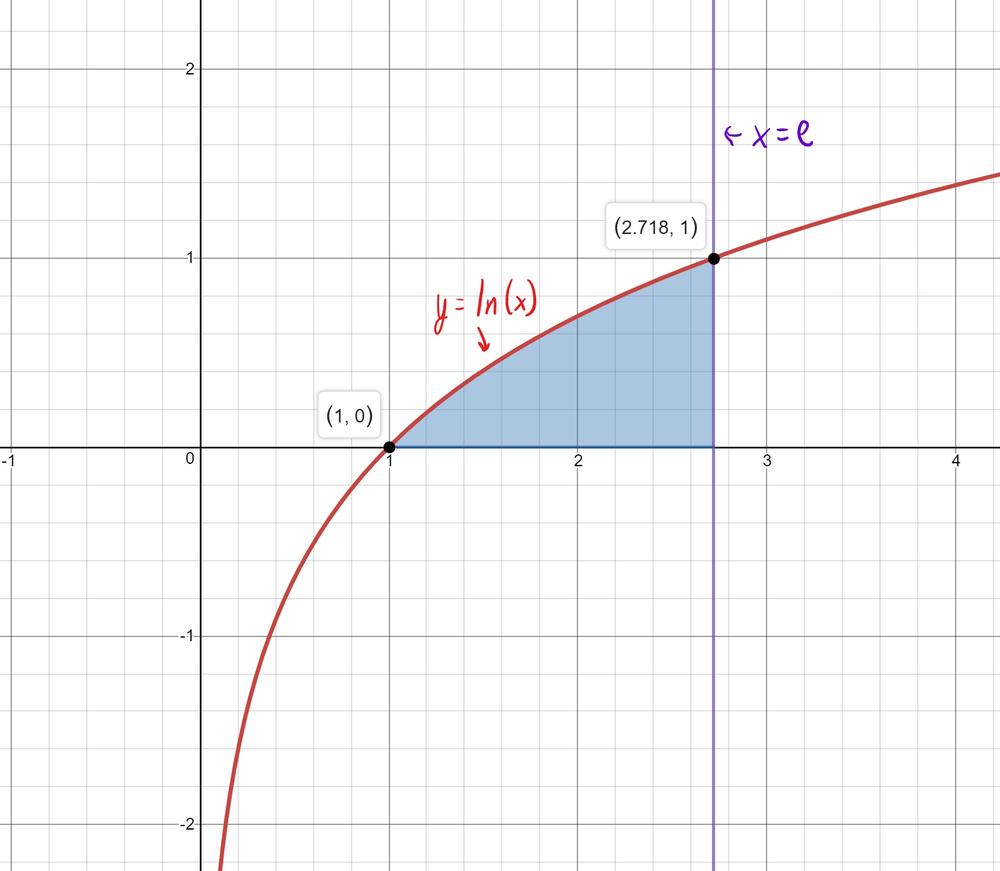


Given The Region Bounded By The Graphs Of Y Ln X Y 0 And X E Find A The Area Of The Region B The Volume Of The Solid



Implicit Derivation Of Logarithmic Function Y Ln X 2 Y 2 Youtube



5 5 The Differentiation Of Logarithmic Functions Let Y Ln X X 0



Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube



Compute The Divergence Of The Vector Field F X Y Z Ln X 2 Y 2 I Math Videos F X Computer



How Do You Find The Volume Of The Solid Generated By Revolving The Region Bounded By The Graph Of Y Ln X The X Axis The Lines X 1 And X



Solved F X Y Xe Y 1 F X Y Ln X Y 7 8 Find T Chegg Com
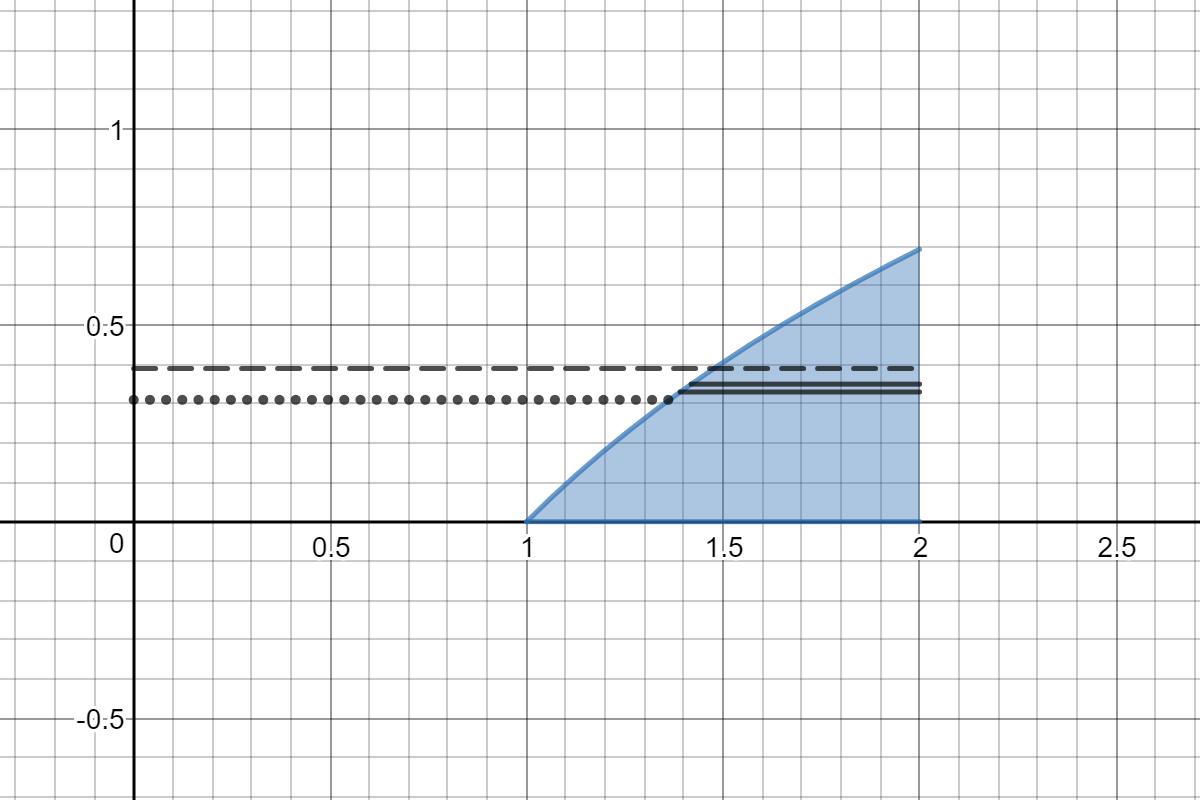


How Do You Find The Volume Bounded By Y Ln X And The Lines Y 0 X 2 Revolved About The Y Axis Socratic



Ejercicios De Calculo Vectorial Pagina 2 Monografias Com



First Order Partial Derivatives Of F X Y Ln X 4 Y 4 Partial Derivative Math Videos Maths Exam



Answered 54 Y Ln X Cos Cos X 3d Bartleby



How To Find The Domain And Range Of F X Y Ln Xy 2 Youtube



Solutions To Midterm 1 Practice Problems



Calc 501 1000 By James Bardo Issuu



Y Ln X Sqrt X 2 A 2 Find Dy Dx Youtube



0 件のコメント:
コメントを投稿